算法-排序算法

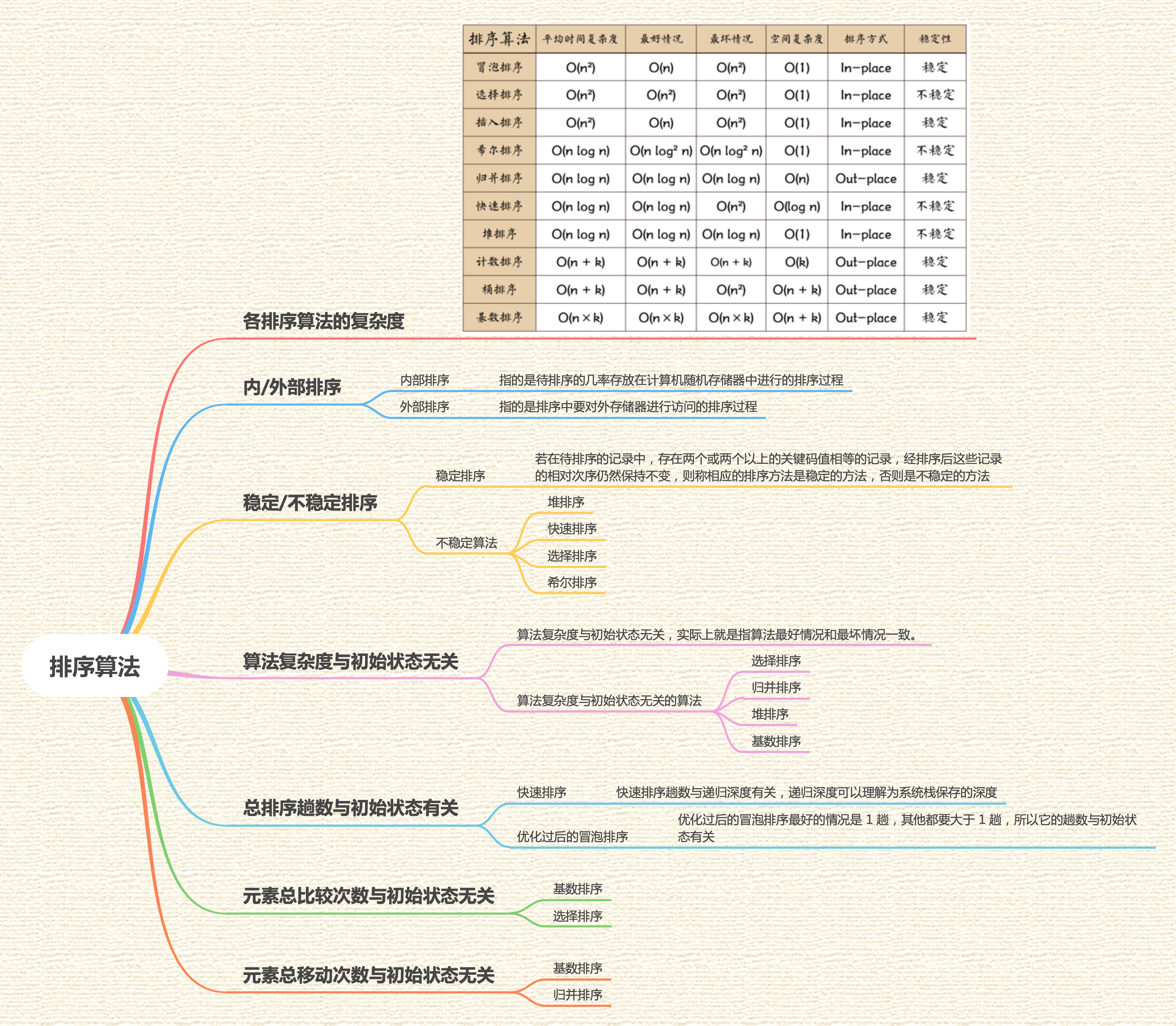
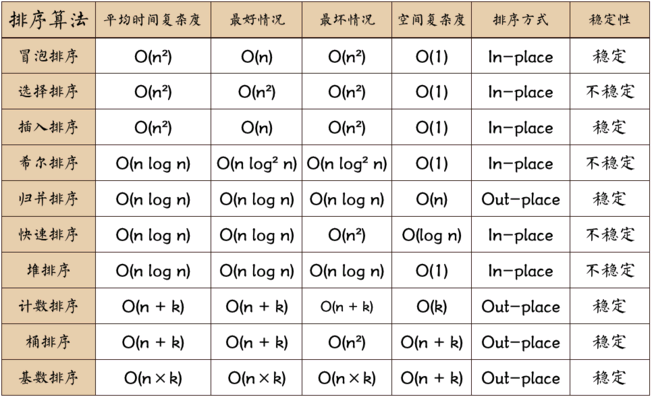
各排序算法的复杂度

归并排序需要外部数组进行存储，来存放对半分隔的临时数组，所以是外部排序。

稳定排序:若在待排序的记录中，存在两个或两个以上的关键码值相等的记录，经排序后这些记录的相对次序仍然保持不变，则称相应的排序方法是稳定的方法，否则是不稳定的方法。

判断算法是否稳定主要是看算法是否比较相邻元素，交换相邻元素，如果一个算法既比较相邻元素，又交换相邻元素，那么相等的元素不会彼此进行交换，那么相对次序永远不会变。

例如针对于数组 [5,….,5]，第一个 5 排在第二个 5 前面，那么当序列变为 […,5,5…] 时，两个 5 之间不会交换位置，那么相对次序肯定就不会变了，所以算法稳定。

堆排序比较的不是相邻元素，也不是交换相邻元素，所以不稳定。

快排比较的是相邻的元素，但是交换的不是相邻元素，所以不稳定。

选择排序比较的不是相邻元素，也不是交换相邻元素，所以不稳定。

希尔排序比较的不是相邻元素，也不是交换相邻元素，所以不稳定。

所以不稳定算法有：

算法复杂度与初始状态无关，实际上就是指算法最好情况和最坏情况一致。

计数排序有点特殊，虽然最好情况和最坏情况复杂度一致，都为 O(n+k) 但是计数排序实际上依赖于数字的分布，如果所有数字比较集中的话，那么算法效率比较高，如果数字差距比较大的话，例如包含 1 和 10^9 这样的数字的话，那效率会比较差。

所以排除计数排序之后，算法复杂度与初始状态无关的算法有以下几种：

快速排序趟数与递归深度有关，递归深度可以理解为系统栈保存的深度。

例如{50,10,90,30,70,40,80,60,20}在快速排序过程中的递归过程。由于我们的第一个关键字是 50，正好是待排序的序列的中间值，因此递归树是平衡的，此时性能也比较好。

例如{10,20,30,40,50,60,70,80,90}第一个关键字是 10，构造出的递归树是不平衡的，性能会比较差，递归树的高度也是比较高度的，排序的趟数也是较平衡状态的要更高。

因为优化过后的冒泡排序最好的情况是 1 趟，其他都要大于 1 趟，所以它的趟数与初始状态有关。

基数排序不是基于比较的排序算法，所以它的比较次数为 0，与初始状态无关

选择排序比较次数稳定是 n(n-1)/2，与初始状态无关

基数排序不论初始数组如何排列，都是从个位开始，各自进入自己个位对应的位置，之后也都是一样，所以元素移动次数一样。

归并排序不论一开始的状态如何，最后都是两个数组进入临时数组，移动次数都为两个待合并数组的长度和，然后再将临时数组内元素全部移动到原来数组进行替换。所以元素移动次数与初始状态无关。

Last updated on Nov 29, 2022